快速理解图结构

哥尼斯堡的七桥问题

德国哥尼斯堡有一条大河，哥尼斯堡整个城市被这条大河分割成四块区域，而四块区域全靠架在河上的七座桥互相联系。那么一个人能否从某一陆地出发，在不重复每座桥的情况下，回到原来的出发地？这就是哥尼斯堡七桥问题。

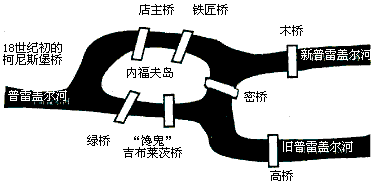
图 20哥尼斯堡七桥问题

瑞士数学家欧拉在1735年对该问题进行论证后，提出没有方法能圆满解决这个问题。欧拉的聪明之处在于把现实世界的问题抽象为数学问题。他把每一座桥视为一条边，桥所连接的两岸和小岛视为顶点，哥尼斯堡七桥问题就变成了一个几何问题——一笔画问题。

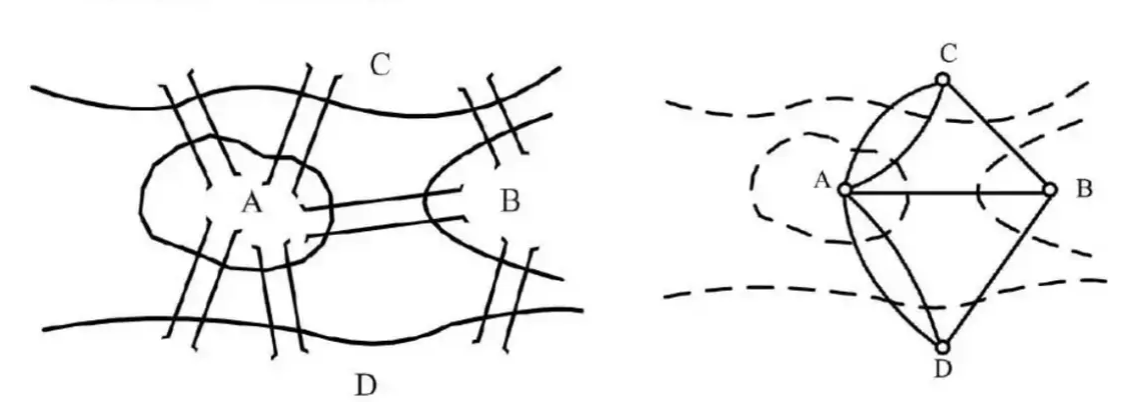
图 1-21 哥尼斯堡七桥问题转换为几何问题

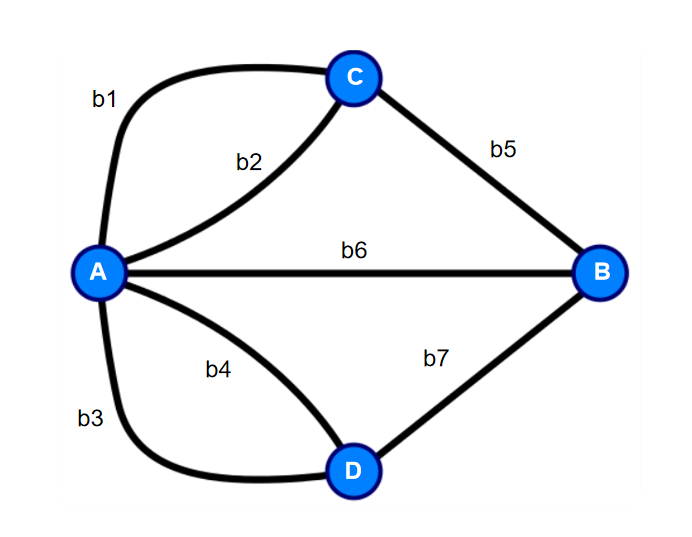
图 1-22一笔画问题

图1-22分别用A、B、C、D四个顶点表示为哥尼斯堡的四个区域，连接四个区域的边分别为b1、b2、b3、b4、b5、b6、b7，这样七桥问题便转化为是否能够用一笔不重复的画出过此七条线的问题了。
若可以画出来，则图1-22所示的图形中必有起点和终点，并且起点和终点应该是同一点。若假设以A为起点和终点，则必有一离开线和对应的进入线，若我们定义进入A的线的条数为入度，离开线的条数为出度，与A有关的线的条数为A的度，则A的出度和入度是相等的，即A的度应该为偶数。即要使得从A出发有解则A的度数应该为偶数，实际上A的度数是5为奇数，于是可知从A出发是无解的。若从B、D、C出发，由于B、D、C的度数都是3，都是奇数，可知从B、D、C出发也是无解的。

图结构的定义

欧拉的研究不仅解决了哥尼斯堡七桥问题，更重要的是，他开创了一种全新的数学结构——图。在图结构中，顶点可以代表任何类型的实体，而边则可以表示实体之间的关系或连接。这种抽象化的表示方法使得图结构成为解决复杂问题的有力工具。

应用计算机来存储和处理图，就形成了图数据结构。图结构是由顶点（或称为节点）和边组成的集合。顶点表示对象或实体，而边则表示这些对象或实体之间的关系。

图 1-23一个简单的交通网络图

图1-23描述了几个城市之间的交通网络图，图的顶点是城市，图的边是连接两个城市的公路。

图的定义

图由顶点集V(G)和边集E(G)组成，记为G=(V,E)。其中E(G)是边的有限集合，边是顶点的无序对（无向图）或有序对（有向图）。
例如在图1-23中：
V(G) = {北京，西安，郑州，徐州，成都，广州，上海}
E(G) = { (北京，西安)，(北京，徐州)，(北京，郑州)，(西安，郑州)，(西安，成都)，(广州，成都)，(广州，上海)，(徐州，上海)，(郑州，广州) }

顶点的度

顶点v的度：与v相关联的边的数目；
顶点v的出度：以v为起点有向边数；
顶点v的入度：以v为终点有向边数；

无向图和有向图

根据边的性质，图结构可以分为无向图和有向图。在无向图中，边没有方向性，表示两个顶点之间的双向关系；而在有向图中，边具有方向性，表示从一个顶点指向另一个顶点的单向关系。

无向边(Edge)：若顶点V1到V2之间的边没有方向，则称这条边为无向边；
有向边：若从顶点V1到V2的边有方向，则称这条边为有向边。

图1-23是无向图，表示两个城市之间的公路是双向的，其顶点只有度，没有出度和入度。例如顶点北京的度是3，顶点上海的度是2，……。

若图1-23的边表示铁路，两个城市间的铁路或双向或单向，则图1-23会演变为有向图1-24：

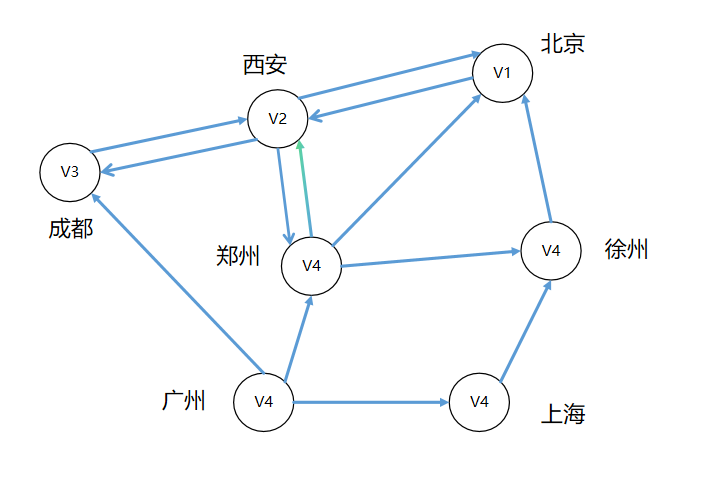
图 1-24一个简单的铁路网络有向图
图1-24为有向图，顶点V1的度是4，出度是1，入度是3，顶点V4的度是5，出度是3，入度是2，顶点的上海的度是2，出度是1入度是2，……。

在有向图中，顶点对(v1,v2)和(v2, v1)表示不同的边，即使它们连接的是相同的两个顶点。

图的连通性

在一个图中，若从顶点V(i)到V(j)有路径，则称V(i)和V(j)是连通的，若图中任意两个顶点都是连通的，则该图为连通图。下面分别讨论无向图和有向图的连通性。

无向图

在无向图中，边没有方向。如果图中任意两个顶点都是连通的，那么这个图就是连通图。

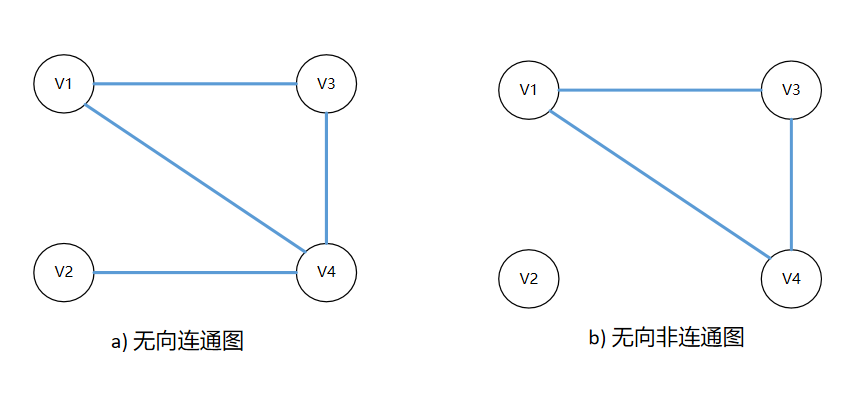
图 1-25 无向连通与非连通示意图

图1-25.a是一个连通图，虽然V1和V2没有直接连接，但从V1到V2存在两条路径，分别是V1-V3-V4和 V1-V4-V2，因此V1和V2是连通的。
图1-25.b是一个非连通图，因为没有任何顶点与V2连通，也找不到任何一条路径连接到V2。虽然图1-25.b是一个非连通图，但图中（V1、V3、V4）构成的子图是一个连通图，该连通图称为图的连通分量。

有向图

有向图的连通性分为弱连通和强连通。
若将有向图中的所有有向边替换为无向边后，图变成连通图，那么这个有向图是弱连通图。若在有向图中，任意两个顶点之间都存在从一个到另一个的有向路径，那么这个图就是强连通图。

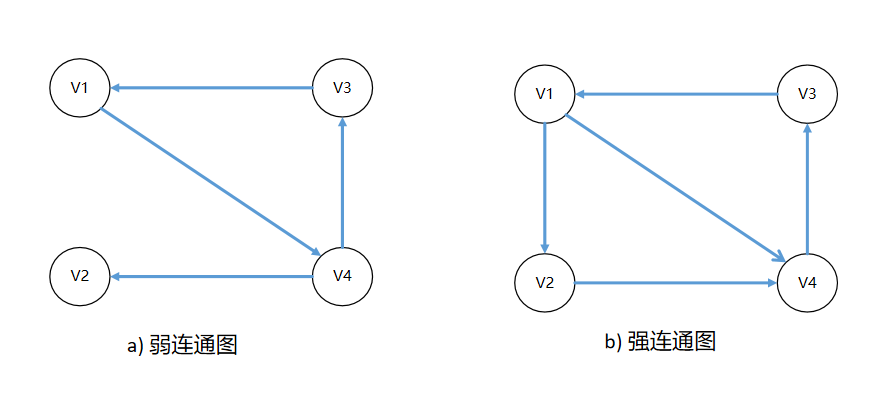
图 1-26有向连通示意图

图1-26a的{(V1，V2),(V2，V4),……}不存在有向路径，但忽略边的有向性后，该图任何顶点之间都是连通的，此图为弱连通图。

图1-26b任何两个顶点之间都存在有向路径，此图为强连通图。图1-26a虽然是弱连通图，但存在（V1, V3, V4）强连通分量。

生成树

对图的所有顶点进行遍历，构成的树结构称为图的生成树。生成树是一个连通且无回路的子图，它包含了原图中所有的节点，但尽可能地减少了边的数量。

生成树是一个图（通常是连通图或无向图）的子图，它满足以下条件：
连通性：生成树中的任意两个顶点之间都存在一条路径。
无环性：生成树中不包含任何环（即闭合的路径）。
包含所有顶点：原图中的所有顶点都出现在生成树中。
边数最少：在所有包含所有顶点的子图中，生成树的边数是最少的。对于含有n个顶点的连通图，其生成树恰好含有n-1条边。

有几种著名的算法可以用来找出图中的生成树，其中最著名的是普里姆（Prim）算法和克鲁斯卡尔（Kruskal）算法。
普里姆算法：从图中的任意一个顶点开始，每次选择与当前生成树距离最短的边，直到所有顶点都包含在生成树中。
克鲁斯卡尔算法：首先对所有边按权重进行排序，然后从小到大依次选择边，如果选择的边不构成环，则将其加入生成树中。

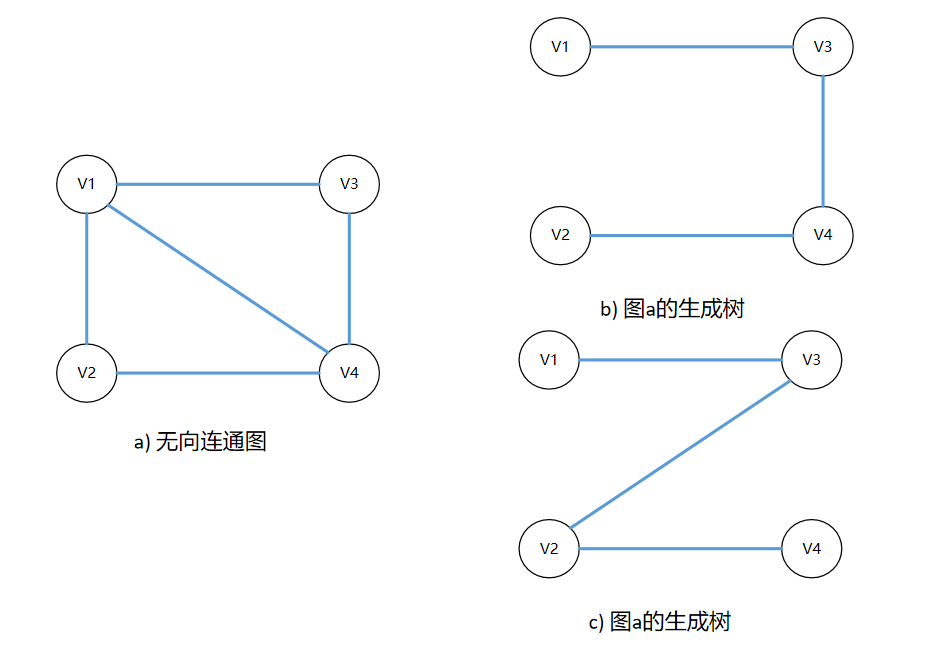
图 1-27生成树示意图

图1-27.b和图1-27.c是图1-27.a的生成树，图1-27.b和图1-27.c满足生成树的条件：任何两个顶点都存在一条路径；不包含回路；包含图1-27.a的所有顶点；边数是最少的，去掉任何一条边后，都不是连通图。