C编程实现：应用正多边形逼近法求π的近似值

正多边形逼近法求π的近似值

正多边形逼近法求π的近似值，其核心思想基于极限理论。设想一个直径为1的圆，若能求出其周长C，则π值可通过π=C/d得出。因此，关键在于准确计算圆的周长C。
此方法，即正多边形逼近，在古代中国已被数学家们采用，用以近似求解圆的周长，当时称为“割圆术”。其精髓在于：圆的内接正多边形边数增加时，其边长更趋近于圆的周长。如下图所示，内接正六边形的周长比内接正四边形的周长更接近外接圆的周长。

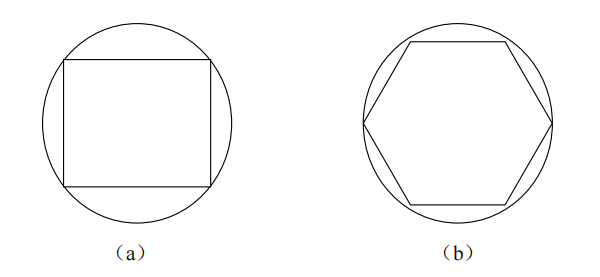
存在一迭代关系：对于单位圆的内接多边形，设其边长为b，边数为i。当边数加倍后，新多边形的边长x可通过公式x=sqrt(2-2*sqrt(1-b^2))/2计算得出，其中sqrt代表开方运算。据此，新多边形的周长为C=2ix，而原多边形的周长为C=bi。

如果最初单位圆的内接多边形为正四边形，其边长sqrt(2)/2，则在此情况下，b=sqrt(2)/2，i=4。当边数加倍后，我们得到一个新的内接正八边形。根据迭代公式，新八边形的边长可以计算为：

通过不断迭代这个过程，我们可以求出内接正十六边形、三十二边形等的边长。每次迭代，都将边数加倍，并使用新的边长值来计算新多边形的周长C，即C = 2ix。
应用正多边形逼近法求π的近似值，在C语言中的实现主要依赖于迭代计算正多边形的边长，并利用这些边长来估计圆的周长，进而求得π的近似值。下面是C语言实现，它考虑了多次迭代，并使用最后一次迭代的多边形周长除以圆的直径来得到π的近似值。

C代码实现

#include <stdio.h>
#include <math.h>

// 函数用于计算给定边数的正多边形在单位圆内的边长
double polygonSideLength(int n) {
if (n < 3) {
printf("多边形边数必须大于等于3\n");
return 0;
}
return sqrt(2) / 2; // 仅作为迭代的起点
}

// 迭代函数，接受当前边长，返回新的边长
double nextPolygonSide(double currentSide) {
return sqrt(2 - 2 * sqrt(1 - currentSide * currentSide));
}

// 使用正多边形逼近法求π的近似值
double approximatePi(int iterations) {
double side = sqrt(2) / 2; // 从正四边形的边长开始迭代
for (int i = 0; i < iterations; i++) {
side = nextPolygonSide(side); // 计算新的边长
}
return 2 * side; // 简化的π近似值
}

int main() {
int iterations = 10; // 迭代次数，可以根据需要调整
double piApprox = approximatePi(iterations);
printf("Approximation of Pi after %d iterations: %f\n", iterations, piApprox);

return 0;
}

知识拓展

单位圆是指半径为1的圆。在单位圆中，内接正四边形的边长可以通过其顶点与圆心连线（即半径）和正四边形的性质来计算。由于正四边形的每个内角都是90度（或说每个外角都是90度，与圆心角相对应），并且它均匀地将圆分为四等份，因此每条边都会与半径形成一个45度的角。

利用三角函数，特别是正弦函数，我们可以计算这个边长。在单位圆中，半径为1，所以边长 S可以通过sin45度来计算，即：